Problem

A conveyor belt has packages that must be shipped from one port to another within days days.

The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.

Example 1:

Input: weights = [1,2,3,4,5,6,7,8,9,10], days = 5 Output: 15 Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this: 1st day: 1, 2, 3, 4, 5 2nd day: 6, 7 3rd day: 8 4th day: 9 5th day: 10 Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.

Example 2:

Input: weights = [3,2,2,4,1,4], days = 3 Output: 6 Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this: 1st day: 3, 2 2nd day: 2, 4 3rd day: 1, 4

Example 3:

Input: weights = [1,2,3,1,1], days = 4 Output: 3 Explanation:1st day: 1 2nd day: 2 3rd day: 3 4th day: 1, 1

Constraints:

• 1 <= days <= weights.length <= 5 * 104
• 1 <= weights[i] <= 500

Solution

You probably wouldn't think binary search would be useful here. You might treat weights as the search space and then realise we've entered a dead end and wasted lots of time.

We're looking for the minimal one among all the feasible capactivites. If we can successfully ship all packages within D days with capacity m, then we can definitely ship them all with any capacity larger than m.

Now we can design our condition function. Let's call it feasible, given an input capacity it returns whether it's possible to ship all packages within D days.

We can run this in a Greedy way. If there's still room for the current package, we put this package onto the conveyor belt, otherwise we wait for the next day to place this package. If the total days needed exceeds D, we return False, otherwise we return True.

Next, we need to initialise our boundary correctly. capacity should be at least max(weights), otherwise the conveyor belt couldn't ship the heaviest package. On the other hand, capacity need not be more thansum(weights), because then we can ship all packages in just one day.

Intuition

An intuitive approach would be to start with checking ship capacity equal to the largest weight in weights, say w. The ship's capacity cannot be smaller than w. We check if it is possible to ship all the packages within days days, using w as the capacity of the ship. If we are able to ship all the packages within the required days, we have w as our required answer.

Otherwise, we increment the capacity and try with w + 1. If we are able to ship the packages within the required days now, w + 1 is the answer. Otherwise, we try with ship's capacity as w + 2.

How long can we go? In the worst case, we might need to choose the capacity of the ship equal to the sum of all the weights in weights and send them all in one day. So, our range starts from the largest weight and goes until the sum of the weights in weights.

This approach will provide the right answer to all the test cases but will indicate that the time limit has been exceeded. Because, in the worst case, we might need to check the ship's capacity from the largest weight to the sum of all elements in weights. The sum of all elements can reach n * 500, since 500 is the maximum weight we can have as per the problem constraints. So, we might need to check O(n⋅500)O(n \cdot 500)O(n⋅500) different values of ship capacity. For each capacity, we need to iterate over all the elements of weights to check whether we can ship the packages in the required number of days or not, this would require O(n)O(n)O(n) time. As a result, the total time required would be O(n⋅n⋅500)=O(n2⋅500)O(n \cdot n \cdot 500) = O(n^2 \cdot 500)O(n⋅n⋅500)=O(n2⋅500) which would lead to TLE.

Let's think of a faster way by making some observations.

If we cannot ship the packages in the required days with capacity A, we can never ship the packages with capacity less than A. Also, if we can ship the packages in the required days with capacity B, we can always ship it with capacity greater than B. So, in such a case, the optimal capacity lies between [A + 1, B] (both inclusive).

A scenario like this where our task is to search for an element X from a given range (L, R) where all values smaller than X do not satisfy a certain condition and all values greater than or equal to X satisfy it (or vice-versa), can be solved optimally with a binary search algorithm. In binary search, we repeatedly divide the solution space where the answer could be in half until the range contains just one element.

Here's how a typical binary search works:

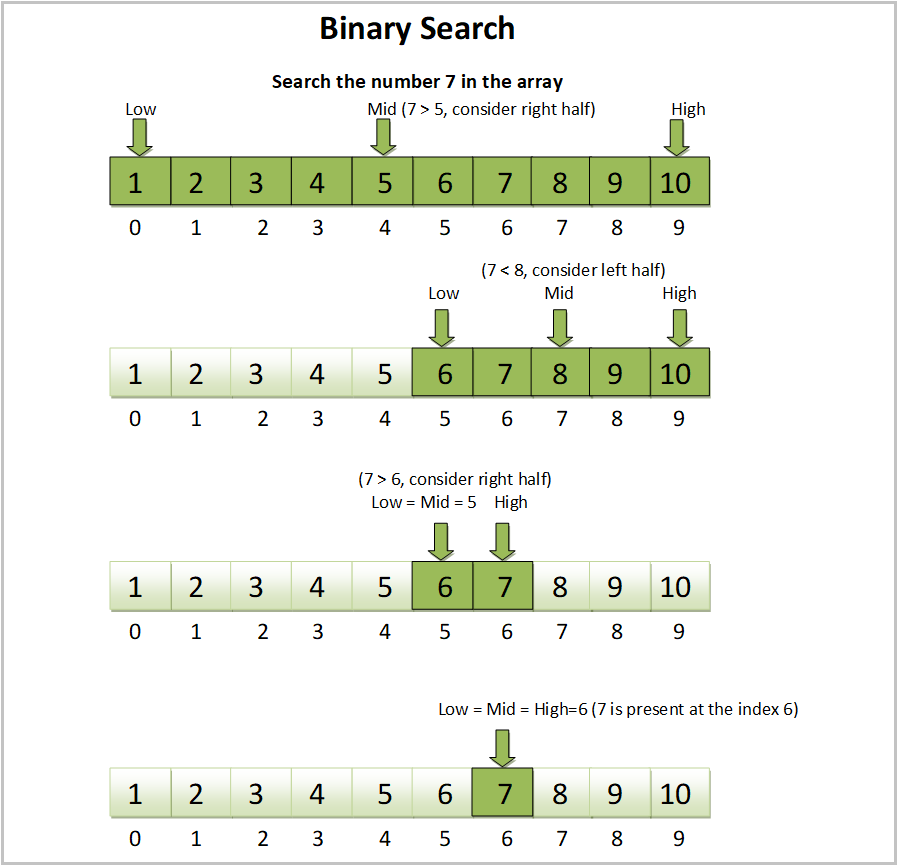
Following the above discussion, we set the starting of the range to the largest weight in weights, say maxWeight and set the ending of the range to the sum of the elements of weights, say totalWeight. We define two variables, l = maxWeight and r = totalWeight to indicate the start and end of the range, respectively. Notice that the end of the range r is always a way to ship the elements within the required days.

Next, we find the middle of the range, mid = (l + r) / 2 and check if using mid capacity we can ship all the packages within days days.

The problem's constraints allow us to use the formula mid = (l + r) / 2 without causing an overflow. Typically, in binary search you should use the safe formula mid = l + (r - l) / 2 to avoid overflow.

If we are able to ship the packages with mid capacity within the required days, we know the answer is at most mid, so we can look for a better answer by moving to the lower half - change r = mid.

Otherwise, if we are not able to ship the packages with mid capacity, we cannot ship the packages with any capacity less than or equal to mid. So, we move to the upper half of the range by moving l = mid + 1.

To check whether we can ship all the packages with a given capacity, c, we create a method and define two variables in it, daysNeeded = 1 and currentLoad = 0 which store the total number of days needed to ship all the weights with c ship capacity and to keep track of how much weight has been placed in the ship on a day, respectively. We iterate over all the weights, and for each weight, we place the weight in the ship and increase its load to currentLoad = currentLoad + weight. We keep on placing the weights until currentLoad > c. If currentLoad exceeds capacity, we cannot keep adding weight and need an additional day. So, we increase the days needed to ship the packages by one, i.e., daysNeeded = daysNeeded + 1 we also set currentLoad = weight as this is the current load for the next day. Finally, if daysNeeded <= days, we return true. Otherwise, we return false.

Algorithm

1. Initialize two integer variables, totalLoad and maxLoad. totalLoad stores the sum of all the elements of weights and maxLoad stores the largest element of weights.
2. Create a method feasible which takes weights, c, days as the parameters and returns true if we can ship all the packages with c capacity.
3. Perform binary search over the range maxLoad to totalLoad.

• Create two variables, l and r, to represent the beginning and end of the range. Set l = maxLoad and r = totalLoad. We can always ship all the weights within days days with r capacity.

1. Then, while l < r:

• Find the midpoint of the range (l, r) in the variable mid = (l + r) / 2.
• Call feasible(weights, mid, days) to see if we can ship all the weights in days days while using mid as the ship's capacity.
• If we can ship the packages with mid as ship's capacity in less than or equal to days days, we move to lower half of the range by setting r = mid.
• Otherwise, if we cannot ship the packages with m capacity in required days, we move to upper half of the range by setting l = mid + 1.

1. Return l (or r) when l = r.

Now we've got all we need to apply our binary search template:

def shipWithinDays(weights: List[int], D: int) -> int:
    def feasible(capacity) -> bool:
        days = 1
        total = 0
        for weight in weights:
            total += weight
            if total > capacity:  # too heavy, wait for the next day
                total = weight
                days += 1
                if days > D:  # cannot ship within D days
                    return False
        return True

    left, right = max(weights), sum(weights)
    while left < right:
        mid = left + (right - left) // 2
        if feasible(mid):
            right = mid
        else:
            left = mid + 1
    return left