❤️ I love the algorithm used here!

Problem

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

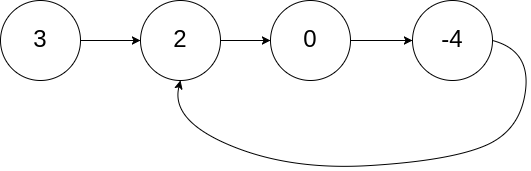
Input: head = [3,2,0,-4], pos = 1 Output: true Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

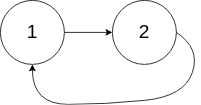
Input: head = [1,2], pos = 0 Output: true Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1 Output: false Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Solution

This uses Floyd's Tortoise and Hare algorithm, the idea is we have tortoise (slow) and hare (fast) pointers.

There is a neat mathematical proof that states if there is a cycle in a list then it must repeat a value twice.

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        # We can do this with 2 pointers
        # fast is "fast" as in it moves 2 steps
        fast = head
        # slow is "slow" as in it moves 1 step
        slow = head
        # since fast moves faster we expect it to end first
        # so we loop based on it
        while fast:
            # if fasts next or next.next is empty
            # we have reached the end and there is no cycle!
            if not fast.next or not fast.next.next:
                break
            # increment slow and fast
            slow = slow.next
            fast = fast.next.next
            # 
            if slow == fast:
                return True
        return False