Problem

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

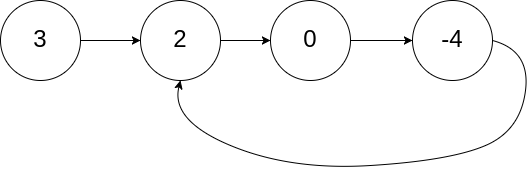
Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

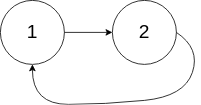
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Solution

Set

A really simple way to do this is to use a set.

We iterate through the list in O(n) time and append nodes to a set.

As we do this, we check if the node we're visiting is already in the set. If it is, we've cycled back around!

class Solution(object):
    def detectCycle(self, head):
        visited = set()

        node = head
        while node is not None:
            if node in visited:
                return node
            else:
                visited.add(node)
                node = node.next

        return None

Tortoise and Hare

We can ues the tortoise and hare algorithm to find the cycle

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if head is None:
            return None
        intersect = self.findIntersection(head)
        if not intersect:
            return None
        # To find the entrance to the cycle, we have two pointers traverse at
        # the same speed -- one from the front of the list, and the other from
        # the point of intersection.
        pointer1 = head
        pointer2 = intersect
        while pointer1 != pointer2:
            pointer1 = pointer1.next
            pointer2 = pointer2.next
        return pointer1

    def findIntersection(self, head):
        fast = head
        slow = head
        while fast is not None and fast.next is not None:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                return slow
        return None