Problem

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

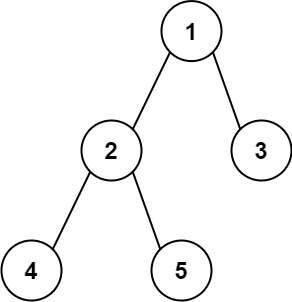
Input: root = [1,2,3,4,5] Output: 3 Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2] Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -100 <= Node.val <= 100

Solution

Bruteforce = take every single node and consider it as the root. We then want to go as far down-ward on the right as much as we can, we then do this for the left side.

One of the best ways to deal with tree questions is to draw the tree physically and go through what your code should be doing.

Typically we do bottom-up recursion with trees so imagine breaking it down into the smallest sub-problem possible (1 or 2 nodes) and making a solution for those nodes, and then building your way up.

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def diameterOfBinaryTree(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        self.diameter = 0
        def dfs(root):
            if not root:
                return 0
            left = dfs(root.left)
            right = dfs(root.right)
            self.diameter = max(self.diameter, left + right)
            return 1 + max(left, right)
        dfs(root)
        return self.diameter