Problem

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3] Output: true

Example 2:

Input: root = [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -231 <= Node.val <= 231 - 1

Solution

On the first sight, the problem is trivial. Let's traverse the tree and check at each step if node.right.val > node.val and node.left.val < node.val. This approach would even work for some trees

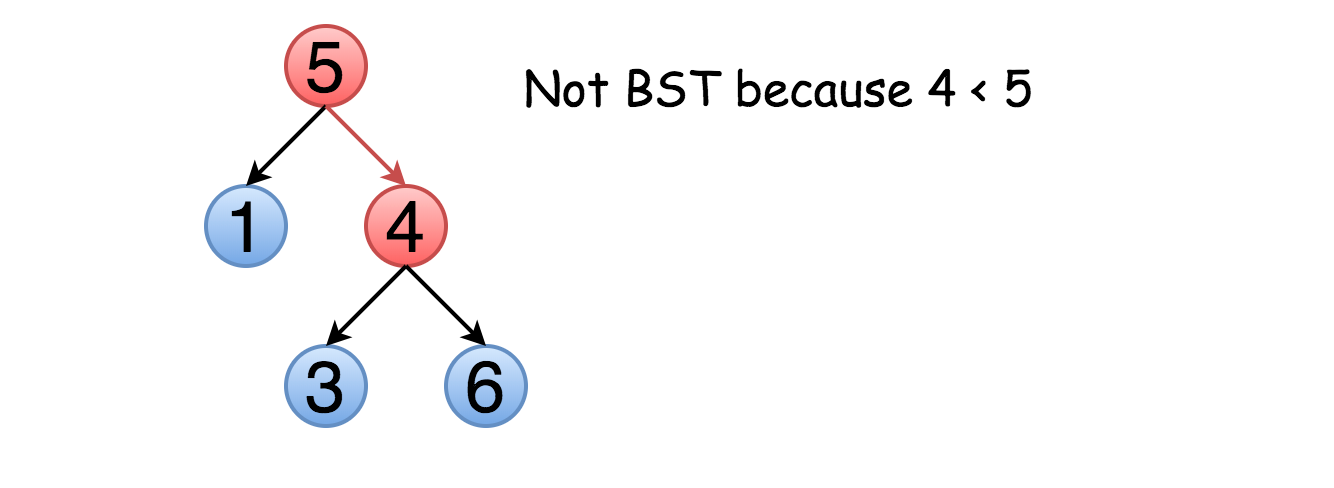
The problem is this approach will not work for all cases. Not only the right child should be larger than the node but all the elements in the right subtree. Here is an example :

That means one should keep both upper and lower limits for each node while traversing the tree, and compare the node value not with children values but with these limits.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        def recurse(node, low, high):
            if not node:
                return True
            if 
            if not (low < node.val < high):
                return False
            return recurse(node.left, low, node.val) and recurse(node.right, node.val, high)
        return recurse(root, -inf, inf)

We need the and at the end of the return because we're doing "is left sub-tree AND right sub-tree valid BSTs?"