🤔 What Is Dynamic Programming With Python Examples

Dynamic programming is breaking down a problem into smaller sub-problems, solving each sub-problem and storing the solutions to each of these sub-problems in an array (or similar data structure) so each sub-problem is only calculated once.
It is both a mathematical optimisation method and a computer programming method.
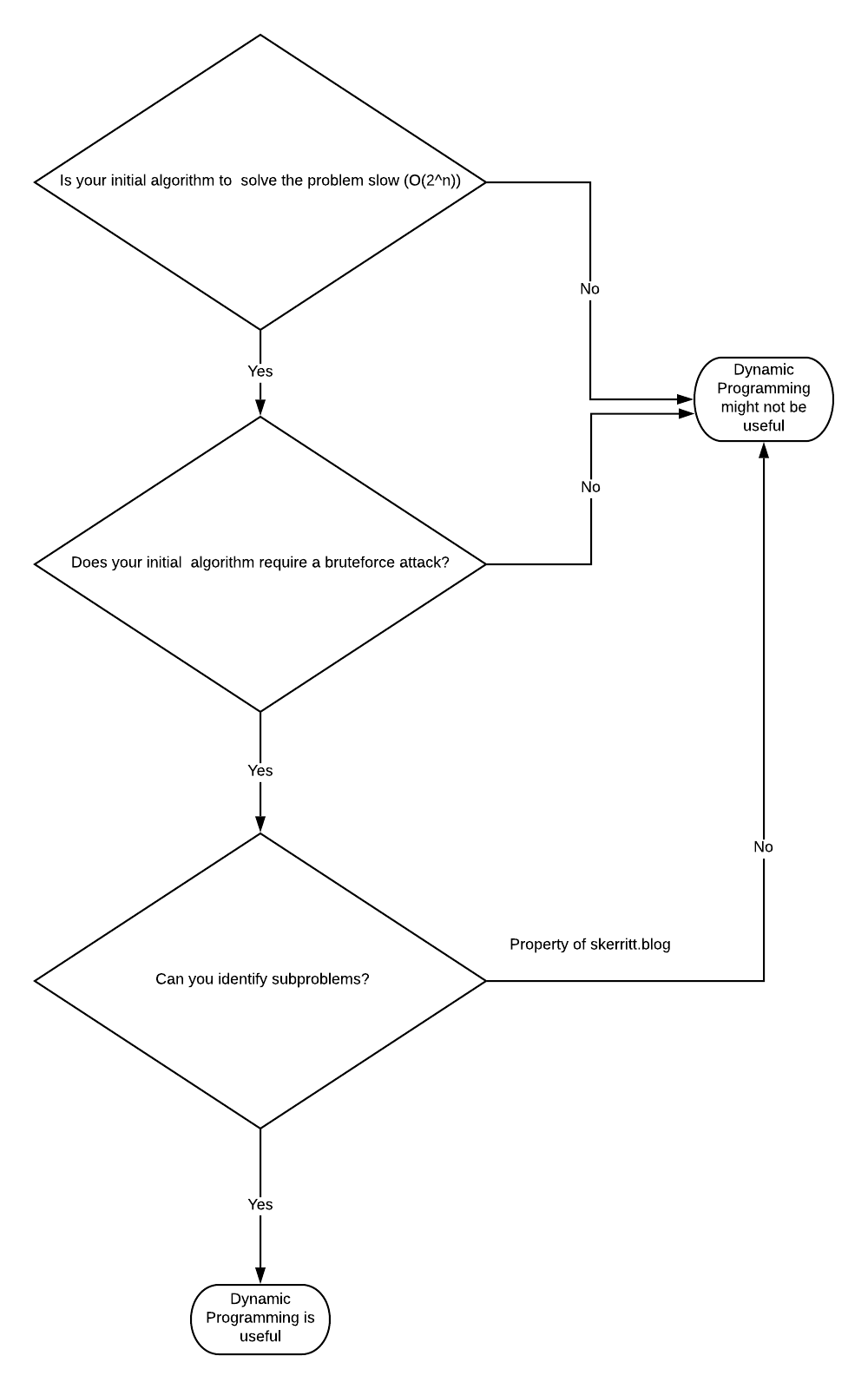
Optimisation problems seek the maximum or minimum solution. The general rule is that if you encounter a problem where the initial algorithm m is solved in O(2n) time, it is better solved using Dynamic Programming.

🤷♀️ Why Is Dynamic Programming Called Dynamic Programming?
Richard Bellman invented DP in the 1950s. Bellman named it Dynamic Programmingbecause at the time, RAND (his employer), disliked mathematical research and didn’t want to fund it. He named it Dynamic Programming to hide the fact he was really doing mathematical research.
Bellman explains the reasoning behind the term Dynamic Programming in his autobiography, Eye of the Hurricane: An Autobiography (1984, page 159). He explains:
“I spent the Fall quarter (of 1950) at RAND.
My first task was to find a name for multistage decision processes. An interesting question is, Where did the name, dynamic programming, come from?
The 1950s were not good years for mathematical research. We had a very interesting gentleman in Washington named Wilson. He was Secretary of Defense, and he actually had a pathological fear and hatred of the word research. I’m not using the term lightly; I’m using it precisely.
His face would suffuse, he would turn red, and he would get violent if people used the term research in his presence. You can imagine how he felt, then, about the term mathematical.
The RAND Corporation was employed by the Air Force, and the Air Force had Wilson as its boss, essentially. Hence, I felt I had to do something to shield Wilson and the Air Force from the fact that I was really doing mathematics inside the RAND Corporation. What title, what name, could I choose?
In the first place I was interested in planning, in decision making, in thinking. But planning, is not a good word for various reasons.
I decided therefore to use the word “programming”. I wanted to get across the idea that this was dynamic, this was multistage, this was time-varying. I thought, let’s kill two birds with one stone.
Let’s take a word that has an absolutely precise meaning, namely dynamic, in the classical physical sense. It also has a very interesting property as an adjective, and that is it’s impossible to use the word dynamic in a pejorative sense.
Try thinking of some combination that will possibly give it a pejorative meaning. It’s impossible.
Thus, I thought dynamic programming was a good name. It was something not even a Congressman could object to. So I used it as an umbrella for my activities.”
☔️ What are Sub-Problems?
Sub-problems are smaller versions of the original problem. Let’s see an example. With the equation below:
$$1 + 2 + 3 + 4$$
We can break this down to:
$$1+2$$
$$3+4$$
Once we solve these two smaller problems, we can add the solutions to these sub-problems to find the solution to the overall problem.
Notice how these sub-problems break down the original problem into components that build up the solution. This is a small example but it illustrates the beauty of Dynamic Programming well. If we expand the problem to adding hundreds of numbers it becomes clearer why we need Dynamic Programming. Take this example:
$$6 + 5 + 3 + 3 + 2 + 4 + 6 + 5$$
We have 6 + 5 twice. The first time we see it, we work out 6+56+5. When we see it the second time we think to ourselves:
“Ah, 6 + 5. I’ve seen this before. It’s 11!”
In Dynamic Programming we store the solution to the problem so we do not need to recalculate it. By finding the solutions for every single sub-problem, we can tackle the original problem itself.
*Memoisation *is the act of storing a solution.
🧠 What is Memoisation in Dynamic Programming?

Let’s see why storing answers to solutions make sense. We’re going to look at a famous problem, Fibonacci sequence. This problem is normally solved in Divide and Conquer.
There are 3 main parts to divide and conquer:
- Divide the problem into smaller sub-problems of the same type.
- Conquer - solve the sub-problems recursively.
- Combine - Combine all the sub-problems to create a solution to the original problem.
Dynamic programming has one extra step added to step 2. This is memoisation.
The Fibonacci sequence is a sequence of numbers. It’s the last number + the current number. We start at 1.
$$1 + 0 = 1$$
$$1 + 1 = 2$$
$$2 + 1 = 3$$
$$3 + 2 = 5$$
$$5 + 3 = 8$$
In Python, this is:
def F(n):
if n == 0 or n == 1:
return n
else:
return F(n-1)+F(n-2)
If you’re not familiar with recursion I have a blog post written for you that you should read first.
Let’s calculate F(4). In an execution tree, this looks like:
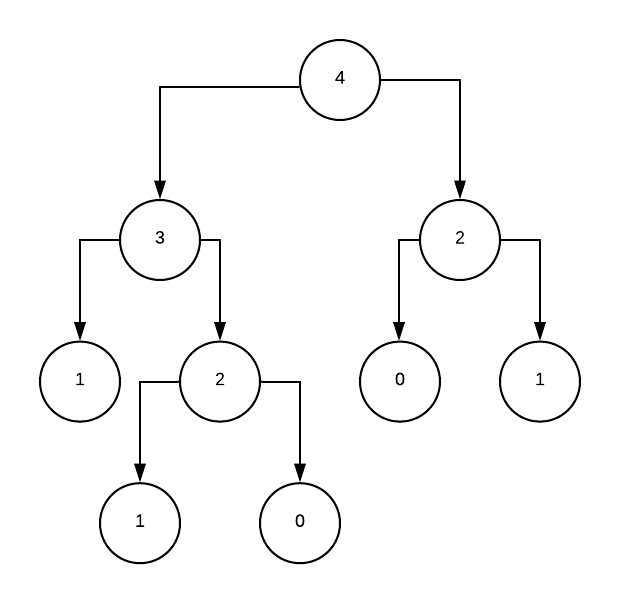
We calculate F(2) twice. On bigger inputs (such as F(10)) the repetition builds up. The purpose of dynamic programming is to not calculate the same thing twice.
Instead of calculating F(2) twice, we store the solution somewhere and only calculate it once.
We’ll store the solution in an array. F[2] = 1. Below is some Python code to calculate the Fibonacci sequence using Dynamic Programming.
def fibonacciVal(n):
memo[0], memo[1] = 0, 1
for i in range(2, n+1):
memo[i] = memo[i-1] + memo[i-2]
return memo[n]
🕵️ How to Identify Dynamic Programming Problems

In theory, Dynamic Programming can solve every problem. The question is then:
“When should I solve this problem with dynamic programming?”
We should use dynamic programming for problems that are between *tractable *and *intractable *problems.
Tractable problems are those that can be solved in polynomial time. That’s a fancy way of saying we can solve it in a fast manner. Binary search and sorting are all fast. Intractable problems are those that run in exponential time. They’re slow. Intractable problems are those that can only be solved by brute-forcing through every single combination (NP hard).
When we see terms like:
“shortest/longest, minimized/maximized, least/most, fewest/greatest, “biggest/smallest”
We know it’s an optimisation problem.
Dynamic Programming algorithms' proof of correctness is usually self-evident. Other algorithmic strategies are often much harder to prove correct. Thus, more error-prone.
When we see these kinds of terms, the problem may ask for a specific number ( “find the minimum number of edit operations”) or it may ask for a result ( “find the longest common subsequence”). The latter type of problem is harder to recognize as a dynamic programming problem. If something sounds like optimisation, Dynamic Programming can solve it.
Imagine we’ve found a problem that’s an optimisation problem, but we’re not sure if it can be solved with Dynamic Programming. First, identify what we’re optimising for. Once we realize what we’re optimising for, we have to decide how easy it is to perform that optimisation. Sometimes, the greedy approach is enough for an optimal solution.
Dynamic programming takes the brute force approach. It Identifies repeated work and eliminates repetition.
Before we even start to plan the problem as a dynamic programming problem, think about what the brute-force solution might look like. Are sub-steps repeated in the brute-force solution? If so, we try to imagine the problem as a dynamic programming problem.
Mastering dynamic programming is all about understanding the problem. List all the inputs that can affect the answers. Once we’ve identified all the inputs and outputs, try to identify whether the problem can be broken into subproblems. If we can identify subproblems, we can probably use Dynamic Programming.
Then, figure out what the recurrence is and solve it. When we’re trying to figure out the recurrence, remember that whatever recurrence we write has to help us find the answer. Sometimes the answer will be the result of the recurrence, and sometimes we will have to get the result by looking at a few results from the recurrence.
Dynamic Programming can solve many problems, but that does not mean there isn’t a more efficient solution out there. Solving a problem with Dynamic Programming feels like magic, but remember that dynamic programming is merely a clever brute force. Sometimes it pays off well, and sometimes it helps only a little.
👩🏫 How to Solve Problems Using Dynamic Programming
Now we have an understanding of what Dynamic programming is and how it generally works. Let’s look at to create a Dynamic Programming solution to a problem. We’re going to explore the process of Dynamic Programming using the Weighted Interval Scheduling Problem.
Pretend you’re the owner of a dry cleaner. You have n customers come in and give you clothes to clean. You can only clean one customer’s pile of clothes (PoC) at a time. Each pile of clothes, i, must be cleaned at some pre-determined start time sisi and some predetermined finish time \(f_i\)
Each pile of clothes has an associated value, \(v_i\), based on how important it is to your business. For example, some customers may pay more to have their clothes cleaned faster. Or some may be repeating customers and you want them to be happy.
As the owner of this dry cleaner, you must determine the optimal schedule of clothes that maximises the total value of this day. This problem is a re-wording of the Weighted Interval scheduling problem.
You will now see 4 steps to solving a Dynamic Programming problem. Sometimes, you can skip a step. Sometimes, your problem is already well-defined and you don’t need to worry about the first few steps.
1. Write the Problem out

Grab a piece of paper. Write out:
- What is the problem?
- What are the sub-problems?
- What would the solution roughly look like?
In the dry cleaner problem, let’s put down into words the subproblems. What we want to determine is the maximum value schedule for each pile of clothes such that the clothes are sorted by start time.
Why sort by start time? Good question! We want to keep track of processes which are currently running. If we sort by finish time, it doesn’t make much sense in our heads. We could have 2 with similar finish times, but different start times. Time moves in a linear fashion, from start to finish. If we have piles of clothes that start at 1 pm, we know to put them on when it reaches 1pm. If we have a pile of clothes that finishes at 3 pm, we might need to put them on at 12 pm, but it’s 1pm now.
We can find the maximum value schedule for piles \(n-1\) through to n. And then for \(n-2\) through to n. And so on. By finding the solution to every single sub-problem, we can tackle the original problem itself. The maximum value schedule for piles 1 through n. Sub-problems can be used to solve the original problem since they are smaller versions of the original problem.
With the interval scheduling problem, the only way we can solve it is by brute-forcing all subsets of the problem until we find an optimal one. What we’re saying is that instead of brute-forcing one by one, we divide it up. We brute force from \(n−1\)through to n. Then we do the same for \(n−2\) through to n. Finally, we have loads of smaller problems, which we can solve dynamically. We want to build the solutions to our sub-problems such that each sub-problem builds on the previous problems.
2. Mathematical Recurrences

I know, mathematics sucks. If you’ll bare with me here you’ll find that this isn’t that hard. Mathematical recurrences are used to:
Define the running time of a divide and conquer (dynamic programming) technique
Recurrences are also used to define problems. If it’s difficult to turn your subproblems into maths, then it may be the wrong subproblem.
There are 2 steps to creating a mathematical recurrence:
1: Define the Base Case
Base cases are the smallest possible denomination of a problem.
When creating a recurrence, ask yourself these questions:
“What decision do I make at step 0?”
It doesn’t have to be 0. The base case is the smallest possible denomination of a problem. We saw this with the Fibonacci sequence. The base was:
- If n == 0 or n == 1, return 1
It’s important to know where the base case lies, so we can create the recurrence. In our problem, we have one decision to make:
- Put that pile of clothes on to be washed
or
- Don’t wash that pile of clothes today
If n is 0, that is, if we have 0 PoC then we do nothing. Our base case is:
if n == 0, return 0
2: What Decision Do I Make at Step n?
Now we know what the base case is, if we’re at step n what do we do? For each pile of clothes that is compatible with the schedule so far. Compatible means that the start time is after the finish time of the pile of clothes currently being washed. The algorithm has 2 options:
- Wash that pile of clothes
- Don’t wash that pile of clothes
We know what happens at the base case, and what happens else. We now need to find out what information the algorithm needs to go backwards (or forwards).
“If my algorithm is at step i, what information would it need to decide what to do in step i+1?”
To decide between the two options, the algorithm needs to know the next compatible PoC (pile of clothes). The next compatible PoC for a given pile, p, is the PoC, n, such that \(s_{n}\) (the start time for PoC n) happens after \(f_{p}\) (the finish time for PoC p). The difference between \(s_{n}\) and \(f_p\) should be minimised.
In English, imagine we have one washing machine. We put in a pile of clothes at 13:00. Our next pile of clothes starts at 13:01. We can’t open the washing machine and put in the one that starts at 13:00. Our next compatible pile of clothes is the one that starts after the finish time of the one currently being washed.
“If my algorithm is at step i, what information did it need to decide what to do in step i-1?”
The algorithm needs to know about future decisions. The ones made for PoC i through n to decide whether to run or not run PoC i-1.
Now that we’ve answered these questions, we’ve started to form a recurring mathematical decision in our minds. If not, that’s also okay, it becomes easier to write recurrences as we get exposed to more problems.
Here’s our recurrence:
$$ OPT(i) = \begin{cases} 0, \quad \text{If i = 0} \\ max{v_i + OPT(next[i]), OPT(i+1)}, \quad \text{if n > 1} \end{cases}$$
Let’s explore in detail what makes this mathematical recurrence. OPT(i) represents the maximum value schedule for PoC i through to n such that PoC is sorted by start times. OPT(i) is our subproblem from earlier.
We start with the base case. All recurrences need somewhere to stop. If we call OPT(0) we’ll be returned with 0.
To determine the value of OPT(i), there are two options. We want to take the maximum of these options to meet our goal. Our goal is the maximum value schedule for all piles of clothes. Once we choose the option that gives the maximum result at step i, we memoize its value as OPT(i).
Mathematically, the two options - run or not run PoC i, are represented as:
$$v_i + OPT(next[n])$$
This represents the decision to run PoC i. It adds the value gained from PoC i to OPT(next[n]), where next[n] represents the next compatible pile of clothing following PoC i. When we add these two values together, we get the maximum value schedule from i through to n such that they are sorted by start time if i runs.
Sorted by start time here because next[n] is the one immediately after \(v_i\), so by default, they are sorted by start time.
$$OPT(i + 1)$$
If we decide not to run i, our value is then OPT(i + 1). The value is not gained. OPT(i + 1) gives the maximum value schedule for i+1 through to n, such that they are sorted by start times.
3. Determine the Dimensions of the Memoisation Array and the Direction in Which It Should Be Filled
The solution to our Dynamic Programming problem is OPT(1). We can write out the solution as the maximum value schedule for PoC 1 through n such that PoC is sorted by start time. This goes hand in hand with the “maximum value schedule for PoC i through to n”.
From step 2:
$$OPT(1) = max(v_1 + OPT(next[1]), OPT(2))$$
Going back to our Fibonacci numbers earlier, our Dynamic Programming solution relied on the fact that the Fibonacci numbers for 0 through to n - 1 were already memoised. That is, to find F(5) we already memoised F(0), F(1), F(2), F(3), F(4). We want to do the same thing here.
The problem we have is figuring out how to fill out a memoisation table. In the scheduling problem, we know that OPT(1) relies on the solutions to OPT(2) and OPT(next[1]). PoC 2 and next[1] have start times after PoC 1 due to sorting. We need to fill our memoisation table from OPT(n) to OPT(1).
We can see our array is one-dimensional, from 1 to n. But, if we couldn’t see that we can work it out another way. The dimensions of the array are equal to the number and size of the variables on which OPT(x) relies. In our algorithm, we have OPT(i) - one variable, i. This means our array will be 1-dimensional and its size will be n, as there are n piles of clothes.
If we know that n = 5, then our memoisation array might look like this:
memo = [0, OPT(1), OPT(2), OPT(3), OPT(4), OPT(5)]
0 is also the base case. memo[0] = 0, per our recurrence from earlier.
4. Coding Our Solution
When I am coding a Dynamic Programming solution, I like to read the recurrence and try to recreate it. Our first step is to initialise the array to size (n + 1). In Python, we don’t need to do this. But you may need to do it if you’re using a different language.
Our second step is to set the base case.
To find the profit with the inclusion of job[i]. we need to find the latest job that doesn’t conflict with job[i]. The idea is to use Binary Search to find the latest non-conflicting job. I’ve copied the code from here but edited it.
First, let’s define what a “job” is. As we saw, a job consists of 3 things:
# Class to represent a job
class Job:
def __init__(self, start, finish, profit):
self.start = start
self.finish = finish
self.profit = profit
Start time, finish time, and the total profit (benefit) of running that job.
The next step we want to program is the schedule.
# The main function that returns the maximum possible
# profit from given array of jobs
def schedule(job):
# Sort jobs according to start time
job = sorted(job, key = lambda j: j.start)
# Create an array to store solutions of subproblems. table[i]
# stores the profit for jobs till arr[i] (including arr[i])
n = len(job)
table = [0 for _ in range(n)]
table[0] = job[0].profit
Earlier, we learnt that the table is 1 dimensional. We sort the jobs by start time, create this empty table and set table[0] to be the profit of job[0]. Since we’ve sorted by start times, the first compatible job is always job[0].
Our next step is to fill in the entries using the recurrence we learnt earlier. To find the next compatible job, we’re using Binary Search. In the full code posted later, it’ll include this. For now, let’s worry about understanding the algorithm.
If the next compatible job returns -1, that means that all jobs before the index, i, conflict with it (so cannot be used). Inclprof means we’re including that item in the maximum value set. We then store it in table[i], so we can use this calculation again later.
# Fill entries in table[] using recursive property
for i in range(1, n):
# Find profit including the current job
inclProf = job[i].profit
l = binarySearch(job, i)
if (l != -1):
inclProf += table[l];
# Store maximum of including and excluding
table[i] = max(inclProf, table[i - 1])
Our final step is then to return the profit of all items up to n-1.
return table[n-1]
The full code can be seen below:
# Python program for weighted job scheduling using Dynamic
# Programming and Binary Search
# Class to represent a job
class Job:
def __init__(self, start, finish, profit):
self.start = start
self.finish = finish
self.profit = profit
# A Binary Search based function to find the latest job
# (before current job) that doesn't conflict with current
# job. "index" is index of the current job. This function
# returns -1 if all jobs before index conflict with it.
def binarySearch(job, start_index):
# https://en.wikipedia.org/wiki/Binary_search_algorithm
# Initialize 'lo' and 'hi' for Binary Search
lo = 0
hi = start_index - 1
# Perform binary Search iteratively
while lo <= hi:
mid = (lo + hi) // 2
if job[mid].finish <= job[start_index].start:
if job[mid + 1].finish <= job[start_index].start:
lo = mid + 1
else:
return mid
else:
hi = mid - 1
return -1
# The main function that returns the maximum possible
# profit from given array of jobs
def schedule(job):
# Sort jobs according to start time
job = sorted(job, key = lambda j: j.start)
# Create an array to store solutions of subproblems. table[i]
# stores the profit for jobs till arr[i] (including arr[i])
n = len(job)
table = [0 for _ in range(n)]
table[0] = job[0].profit;
# Fill entries in table[] using recursive property
for i in range(1, n):
# Find profit including the current job
inclProf = job[i].profit
l = binarySearch(job, i)
if (l != -1):
inclProf += table[l];
# Store maximum of including and excluding
table[i] = max(inclProf, table[i - 1])
return table[n-1]
# Driver code to test above function
job = [Job(1, 2, 50), Job(3, 5, 20),
Job(6, 19, 100), Job(2, 100, 200)]
print("Optimal profit is"),
print(schedule(job))
Congrats! 🥳 We’ve just written our first dynamic program! Now that we’ve wet our feet, let’s walk through a different type of dynamic programming problem.

Knapsack Problem
Imagine you are a criminal. Dastardly smart. You break into Bill Gates’s mansion. Wow, okay!?!? How many rooms is this? His washing machine room is larger than my entire house??? Ok, time to stop getting distracted. You brought a small bag with you. A knapsack - if you will.
You can only fit so much into it. Let’s give this an arbitrary number. The bag will support weight 15, but no more. What we want to do is maximise how much money we’ll make, b.
The greedy approach is to pick the item with the highest value which can fit into the bag. Let’s try that. We’re going to steal Bill Gates’s TV. £4000? Nice. But his TV weighs 15. So… We leave with £4000.
TV = (£4000, 15)
# (value, weight)
Bill Gates has a lot of watches. Let’s say he has 2 watches. Each watch weighs 5 and each one is worth £2250. When we steal both, we get £4500 with a weight of 10.
watch1 = (£2250, 5)
watch2 = (£2250, 5)
watch1 + watch2
>>> (£4500, 10)
In the greedy approach, we wouldn’t choose these watches first. But to us as humans, it makes sense to go for smaller items which have higher values. The Greedy approach cannot optimally solve the {0,1} Knapsack problem. The {0, 1} means we either take the item whole item {1} or we don’t {0}. However, Dynamic programming can optimally solve the {0, 1} knapsack problem.
The simple solution to this problem is to consider all the subsets of all items. For every single combination of Bill Gates’s stuff, we calculate the total weight and value of this combination.
Only those with a weight less than \(w_{max}\) are considered. We then pick the combination which has the highest value. This is a disaster! How long would this take? Bill Gates would come back home far before you’re even 1/3rd of the way there! In Big O, this algorithm takes O(n2) time.
You can see we already have a rough idea of the solution and what the problem is, without having to write it down in maths!
Maths Behind {0, 1} Knapsack Problem
Imagine we had a listing of every single thing in Bill Gates’s house. We stole it from some insurance papers. Now, think about the future. What is the optimal solution to this problem?
We have a subset, L, which is the optimal solution. L is a subset of S, the set containing all of Bill Gates’s stuff.
Let’s pick a random item, N. L either contains N or it doesn’t. If it doesn’t use N, the optimal solution for the problem is the same as 1,2,…,N−1. This is assuming that Bill Gates’s stuff is sorted by value/weight.
Suppose that the optimum of the original problem is not the optimum of the sub-problem. if we have a sub-optimum of the smaller problem then we have a contradiction - we should have an optimum of the whole problem.
If L contains N, then the optimal solution for the problem is the same as 1,2,3,…,N−1. We know the item is in, so L already contains N. To complete the computation we focus on the remaining items. We find the optimal solution to the remaining items.
But, we now have a new maximum allowed weight of \(W_{max} - W_n\). If item N is contained in the solution, the total weight is now the max weight take away item N (which is already in the knapsack).
These are the 2 cases. Either item N is in the optimal solution or it isn’t.
If the weight of item N is greater than \(W_{max}\), then it cannot be included so case 1 is the only possibility.
To better define this recursive solution, let \(S_k =1,2,…,k\) and \(S_0 = ∅\)
Let B[k, w] be the maximum total benefit obtained using a subset of \(S_{k}\). Having total weight at most w.
Then we define B[0, w] = 0 for each \(w \le W_{max}\).
Our desired solution is then B[n, \(W_{max}\)].
$$OPT(i) = \begin{cases} B[k - 1, w], \quad \text{If w < }w_k \\ max{B[k-1, w], b_k + B[k - 1, w - w_k]}, \ \quad \text{otherwise} \end{cases} $$
Tabulation of Knapsack Problem
Okay, pull out some pen and paper. No, really. Things are about to get confusing really fast. This memoisation table is 2-dimensional. We have these items:
(1, 1), (3, 4), (4, 5), (5, 7)
Where the tuples are (weight, value).
We have 2 variables, so our array is 2-dimensional. The first dimension is from 0 to 7. Our second dimension is the values.
And we want a weight of 7 with maximum benefit.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | ||||||||
| (4, 3) | ||||||||
| (5, 4) | ||||||||
| (7, 5) |
The weight is 7. We start counting at 0. We put each tuple on the left-hand side. Ok. Now fill out the table!
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | |||||||
| (4, 3) | 0 | |||||||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
The columns are weight. At weight 0, we have a total weight of 0. At weight 1, we have a total weight of 1. Obvious, I know. But this is an important distinction to make which will be useful later on.
When our weight is 0, we can’t carry anything no matter what. The total weight of everything at 0 is 0.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | ||||||
| (4, 3) | 0 | |||||||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
If our total weight is 1, the best item we can take is (1, 1). As we go down through this array, we can take more items. At the row for (4, 3) we can either take (1, 1) or (4, 3). But for now, we can only take (1, 1). Our maximum benefit for this row then is 1.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | |||||||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
If our total weight is 2, the best we can do is 1. We only have 1 of each item. We cannot duplicate items. So no matter where we are in row 1, the absolute best we can do is (1, 1).
Let’s start using (4, 3) now. If the total weight is 1, but the weight of (4, 3) is 3 we cannot take the item yet until we have a weight of at least 3.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | |||||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
Now we have a weight of 3. Let’s compare some things. We want to take the max of:
$$MAX(4 + T[0][0], 1)$$
If we’re at 2, 3 we can either take the value from the last row or use the item on that row. We go up one row and count back 3 (since the weight of this item is 3).
Actually, the formula is whatever weight is remaining when we minus the weight of the item on that row. The weight of (4, 3) is 3 and we’re at weight 3. 3−3=03−3=0. Therefore, we’re at T[0][0]. T[previous row's number][current total weight - item weight].
$$MAX(4 + T[0][0], 1)$$
The 1 is because of the previous item. The max here is 4.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | ||||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
$$max(4 + t[0][1], 1)$$
The total weight is 4, the item weight is 3. 4 - 3 = 1. The previous row is 0. t[0][1].
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | |||
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
I won’t bore you with the rest of this row, as nothing exciting happens. We have 2 items. And we’ve used both of them to make 5. Since there are no new items, the maximum value is 5.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | |||||||
| (7, 5) | 0 |
Onto our next row:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | ||||
| (7, 5) | 0 |
Here’s a little secret. Our tuples are ordered by weight! That means that we can fill in the previous rows of data up to the next weight point. We know that 4 is already the maximum, so we can fill in the rest.. This is where memoisation comes into play! We already have the data, why bother re-calculating it?
We go up one row and head 4 steps back. That gives us:
$$max(4 + T[2][0], 5)$$.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | |||
| (7, 5) | 0 |
Now we calculate it for total weight 5.
$$max(5 + T[2][1], 5) = 6$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | ||
| (7, 5) | 0 |
We do the same thing again:
$$max(5 + T[2][2], 5) = 6$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | |
| (7, 5) | 0 |
Now we have total weight 7. We choose the max of:
$$max(5 + T[2][3], 5) = max(5 + 4, 5) = 9$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 |
If we had a total weight of 7 and we had the 3 items (1, 1), (4, 3), (5, 4) the best we can do is 9.
Since our new item starts at weight 5, we can copy from the previous row until we get to weight 5.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 |
We then do another max.
Total weight - new item’s weight. This is 5−5=0. We want the previous row at position 0.
$$max(7 + T[3][0], 6)$$
The 6 comes from the best on the previous row for that total weight.
$$max(7 + 0, 6) = 7$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 |
$$max(7 + T[3][1], 6) = 8$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 |
$$max(7+T[3][2], 9) = 9$$
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
9 is the maximum value we can get by picking items from the set of items such that the total weight is≤7≤7.
Finding the Optimal Set for {0, 1} Knapsack Problem Using Dynamic Programming
Now, what items do we actually pick for the optimal set? We start with this item:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
We want to know where the 9 comes from. It's coming from the top because the number directly above 9 on the 4th row is 9. Since it's coming from the top, the item (7, 5) is not used in the optimal set.
Where does this 9 come from?
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
This 9 is not coming from the row above it. **Item (5, 4) must be in the optimal set.**
We now go up one row and go back 4 steps. 4 steps because the item, (5, 4), has weight 4.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
4 does not come from the row above. The item (4, 3) must be in the optimal set.
The weight of item (4, 3) is 3. We go up and we go back 3 steps and reach:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| (1, 1) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (4, 3) | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| (5, 4) | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| (7, 5) | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
As soon as we reach a point where the weight is 0, we're done. Our two selected items are (5, 4) and (4, 3). The total weight is 7 and our total benefit is 9. We add the two tuples together to find this out.
Let’s begin coding this.
Coding {0, 1} Knapsack Problem in Dynamic Programming With Python
Now we know how it works, and we’ve derived the recurrence for it - it shouldn’t be too hard to code it. If our two-dimensional array is i (row) and j (column) then we have:
if j < wt[i]:
If our weight j is less than the weight of item i (i does not contribute to j) then:
if j < wt[i]:
T[i][j] = T[i - 1][j]
else:
# weight of i >= j
T[i][j] = max(val[i] + t[i - 1][j-wt(i), t[i-1][j])
# previous row, subtracting the weight of the item from the total weight or without including ths item
This is what the core heart of the program does. I’ve copied some code from here to help explain this. I’m not going to explain this code much, as there isn’t much more to it than what I’ve already explained. If you’re confused by it, leave a comment below or email me 😁
# Returns the maximum value that can be put in a knapsack of
# capacity W
def knapSack(W , wt , val , n):
# Base Case
if n == 0 or W == 0:
return 0
# If weight of the nth item is more than Knapsack of capacity
# W, then this item cannot be included in the optimal solution
if (wt[n-1] > W):
return knapSack(W , wt , val , n-1)
# return the maximum of two cases:
# (1) nth item included
# (2) not included
else:
return max(val[n-1] + knapSack(W-wt[n-1] , wt , val , n-1),
knapSack(W , wt , val , n-1))
# To test above function
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print(knapSack(W , wt , val , n))
# output 220
Time Complexity of a Dynamic Programming Problem

Time complexity is calculated in Dynamic Programming as:
$$Number \; of \; unique \; states * time \; taken \; per \; state$$
For our original problem, the Weighted Interval Scheduling Problem, we had n piles of clothes. Each pile of clothes is solved in constant time. The time complexity is:
$$O(n) + O(1) = O(n)$$
I’ve written a post about Big O notation if you want to learn more about time complexities.
With our Knapsack problem, we had n number of items. The table grows depending on the total capacity of the knapsack, our time complexity is:
$$O(nw)$$
Where n is the number of items, and w is the capacity of the knapsack.
I’m going to let you in on a little secret. It’s possible to work out the time complexity of an algorithm from its recurrence. You can use something called the Master Theorem to work it out. This is the theorem in a nutshell:
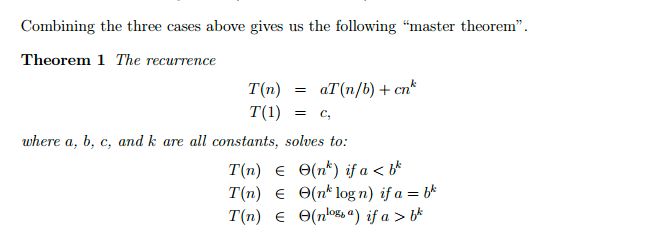
Now, I’ll be honest. The master theorem deserves a blog post of its own. For now, I’ve found this video to be excellent:
Dynamic Programming vs Divide & Conquer vs Greedy
Dynamic Programming & Divide and Conquer are similar. Dynamic Programming is based on Divide and Conquer, except we memoise the results.
But, Greedy is different. It aims to optimise by making the best choice at that moment. Sometimes, this doesn’t optimise the whole problem. Take this question as an example. We have 3 coins:
1p, 15p, 25p
And someone wants us to give a change of 30p. With Greedy, it would select 25, then 5 * 1 for a total of 6 coins. The optimal solution is 2 * 15. Greedy works from largest to smallest. At the point where it was at 25, the best choice would be to pick 25.
| Greedy vs Divide & Conquer vs Dynamic Programming | ||
|---|---|---|
| Greedy | Divide & Conquer | Dynamic Programming |
| Optimises by making the best choice at the moment | Optimises by breaking down a subproblem into simpler versions of itself and using multi-threading & recursion to solve | Same as Divide and Conquer, but optimises by caching the answers to each subproblem as not to repeat the calculation twice. |
| Doesn't always find the optimal solution, but is very fast | Always finds the optimal solution, but is slower than Greedy | Always finds the optimal solution, but could be pointless on small datasets. |
| Requires almost no memory | Requires some memory to remember recursive calls | Requires a lot of memory for memoisation / tabulation |
Tabulation (Bottom-Up) vs Memoisation (Top-Down)

There are 2 types of dynamic programming. Tabulation and Memoisation.
Memoisation (Top-Down)
We’ve computed all the subproblems but have no idea what the optimal evaluation order is. We would then perform a recursive call from the root and hope we get close to the optimal solution or obtain proof that we will arrive at the optimal solution. Memoisation ensures you never recompute a subproblem because we cache the results, thus duplicate sub-trees are not recomputed.
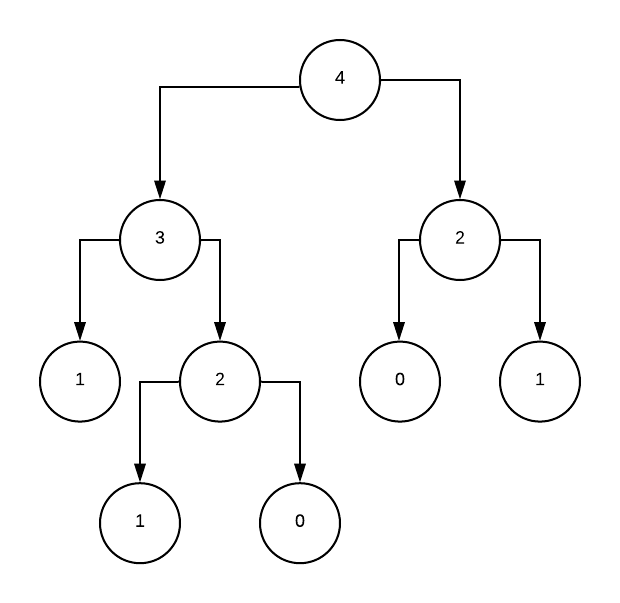
From our Fibonacci sequence earlier, we start at the root node. The subtree F(2) isn’t calculated twice.
This starts at the top of the tree and evaluates the subproblems from the leaves/subtrees back up towards the root. Memoisation is a top-down approach.
Tabulation (Bottom-Up)
We’ve also seen Dynamic Programming being used as a ‘table-filling’ algorithm. Usually, this table is multi-dimensional. This is like memoisation but with one major difference. We have to pick the exact order in which we will do our computations. The knapsack problem we saw, we filled in the table from left to right - top to bottom. We knew the exact order in which to fill the table.
Sometimes the ‘table’ is not like the tables we’ve seen. It can be a more complicated structure such as trees. Or specific to the problem domain, such as cities within flying distance on a map.
Tabulation & Memosation - Advantages and Disadvantages
Generally speaking, memoisation is easier to code than tabulation. We can write a ‘memoriser’ wrapper function that automatically does it for us. With tabulation, we have to come up with an order.
Memoisation has memory concerns. If we’re computing something large such as F(10^8), each computation will be delayed as we have to place them into the array. And the array will grow in size very quickly.
Either approach may not be time-optimal if the order we happen to visit subproblems is not optimal. If there is more than one way to calculate a subproblem (normally caching would resolve this, but it’s theoretically possible that caching might not in some exotic cases). Memoisation will usually add on our time complexity to our space complexity. For example, with tabulation we have more liberty to throw away calculations, like using tabulation with Fib lets us use O(1) space, but memoisation with Fib uses O(N) stack space).
| Memoisation vs Tabulation | ||
|---|---|---|
| Tabulation | Memoisation | |
| Code | Harder to code as you have to know the order | Easier to code as functions may already exist to memoise |
| Speed | Fast as you already know the order and dimensions of the table | Slower as you're creating them on the fly |
| Table completeness | The table is fully computed | Table does not have to be fully computed |
Conclusion
Most of the problems you’ll encounter within Dynamic Programming already exist in one shape or another. Often, your problem will build on from the answers for previous problems. Here’s a list of common problems that use Dynamic Programming.
I hope that whenever you encounter a problem, you think to yourself “can this problem be solved with ?” and try it.
