Functions cheat sheet
I suggest making your own flashcards to study, but if you don’t want to you can use my flashcard deck here.
https://quizlet.com/gb/240513173/functions-flash-cards/
A function is just like a function in programming. It takes an input, performs some maths on it, and then outputs the result.
The syntax of a function is f(x) = 2 * x. This means that given x, the function will return 2*x.
A function cannot have more than one output if given a single input. However, multiple inputs can lead to the same output.
Functions can be written in two ways, either f(x) = 2 * x or f: R→ R which defines the input and output to be real numbers.
Domain, Codomain, Range
Let function f(x) = 2x. The set, x, is the Domain; the range of all possible inputs. The set 2x is the codomain. The values produced by the function is the range.
In another syntax, f: A → B. A is called the domain, B is the **co-domain **and the **range **of f(A) is F(A) = {f(x) | x ∈ A}
Finding the domain of a function
It is best to show an example of how to find the domain of a function.
f(x) = sqrt(2x-8) We know that the domain of a function is the set of all possible inputs into a function. We know that the above function is only defined when it’s taking the square root of a non-negative number so it’s only going to be defined when: 2x-8 ≥ 0. Now this is a simple algebraic problem to find x. 2x ≥ 8 x ≥ 4So the domain here is the set of all real numbers ≥ 4.
Sometimes it is easier to find what cannot be in the domain than to find every item in the domain.
Given the function f(x) = 2/x-3, let’s try find the range.
Is there anything that X CANNOT be? Yes! If X is 0 it would cause an error as you cannot divide by 0!
Types of functions
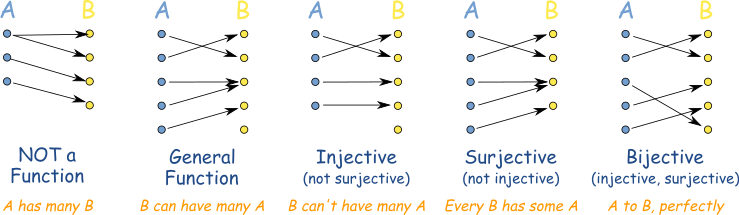
Label the left-hand set A and the right-hand set B and ignore the lines.
A has many B
Not a function, because function inputs cannot map to more than one output.
B can have many A
It is a function because a single output can be produced from different inputs.
B can’t have many A (Injective)
Not all outputs of B can be produced by A.
Every B has some A (Surjective)
Every output in B has at least one input in A, sometimes more.
A to B, perfectly (Bijective)
Bijective is the combination of injective and surjective. Every A matches perfectly to an output.
https://www.mathsisfun.com/sets/injective-surjective-bijective.html
Cardinality of sets
The cardinality of a set is how many items are in the set, denoted as |a|
Powersets
The powerset is the set containing every single subset of set A, where A is any set. The powerset of a = {1, 2, 3} is:
Pow(A)= { {1}, {2}, {3}, {1,2}, {1,3}, {2, 3}, {1, 2, 3}, {Ø} }
The cardinality of a power set is always 2^n where n is |a|. The same cardinality rule applies to bit vector sets.
Infinite sets
Infinite sets can also be bijective, injective or surjective.
Uncountable sets
There exists sets that are not countable, such as Cantor’s set derived from Cantor’s diagonal argument.
The Pigeon Hole Principle
The Pigeon Hole Principle states that if |A| > |B| then at least one value of F occurs more than once.
In other words, if there are N holes and we have N+1 pigeon then 2 pigeons must occupy the same hole.
