This Simple Trick will Save you Hours of Expanding Binomials
Ever wanted to know how to expand (a+b)¹⁸⁷? Well now you can!
What is a Binomial Coefficient?
First, let’s start with a binomial. A binomial is a polynomial with two terms typically in the format (a+b)²
A binomial coefficient is raising a binomial to the power of n, like so (a+b)^n
We all remember from school that (a+b)² = a² + 2ab + b², but what is (a+b)⁸? This where the binomial formula comes in handy.
Binominal Theorem
The Binomial Theorem is the expected method to use for finding binomial coefficients because it is how a computer would compute it. The theorem is as follows:
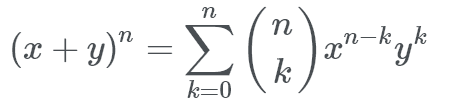
Luckily for us, this formula is the same as another formula we’ve seen, according to here.
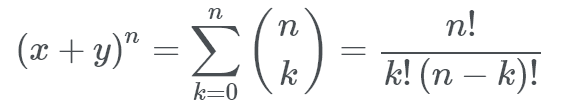
The combinations formula! Let’s try an example.
Example
What is the coefficient of x⁶ in (1+x)⁸?
Simply plug this into the formula like so
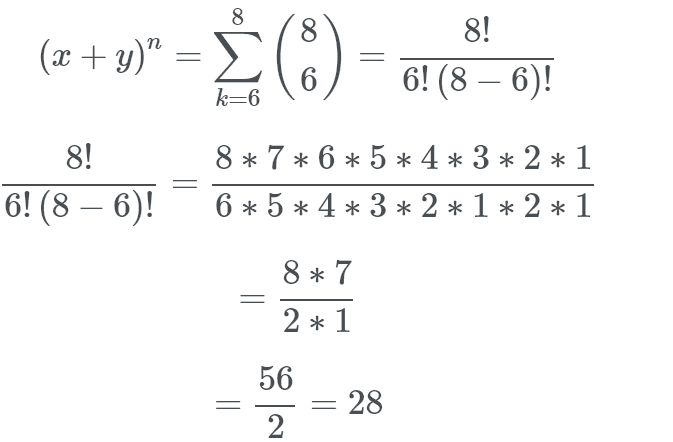
Something that may confuse people is, how do we work out what n and k are? Well, we have n objects overall and we want to choose k of them. For binomial / combinatorics sums it helps to think “(combinations of) X taken in sets of Y” where x > y for obvious reasons, in this case “(combinations of) 8 taken in sets of 6”.
Pascal’s Triangle
Pascal’s triangle is a triangle created by starting off with a 1, starting every line and ending every line with a 1 and adding the numbers above to make a new number; as seen in this gif.
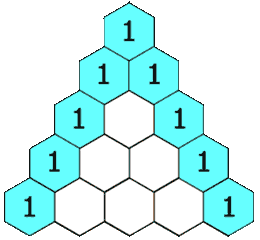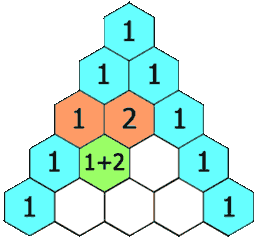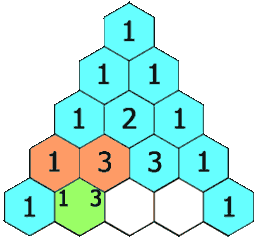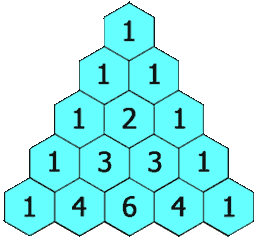
From Wikipedia No one could ever explain a maths topic as well as Numberphile, so here’s a Numberphile video on it:
Example
Let’s solve the example from earlier using Pascal’s triangle.

Triangle we want Pascal’s triangle always starts counting from 0, so to solve 8C6 (8 choose 6) we simply count 8 rows down, then 6 across. So the row here is the line of the number 1’s on the left hand side, and we start counting from 0. So the eigth row is the one that starts with 1, 8. Notice how the second inner column defines what row we’re on.
Now we count 6 across which is… 28. We just found the binomial coefficient using a super neat and easy to draw up triangle. Of course, the hardest part is adding together all the numbers and if the coefficient is large it may be easier to just use the Binomial theorem, but this method still exists and is useful if you’ve forgotten the binomial theorem.
